Độ phức tạp của thuật toán - Làm thế nào để tìm độ phức tạp thời gian của một thuật toán?

1. Độ phức tạp của thuật toán là gì?

Độ phức tạp của thuật toán đề cập đến lượng tài nguyên (ví dụ như thời gian hoặc bộ nhớ) cần thiết để giải quyết vấn đề hoặc thực hiện một nhiệm vụ. Thước đo độ phức tạp phổ biến nhất là độ phức tạp về thời gian, đề cập đến lượng thời gian mà thuật toán cần để tạo ra kết quả dựa theo kích thước của đầu vào. Độ phức tạp của bộ nhớ đề cập đến lượng bộ nhớ được sử dụng trong một thuật toán. 

Độ phức tạp thuật toán là hàm mô tả tính hiệu quả của thuật toán xét về lượng dữ liệu mà thuật toán cần phải xử lý. Bạn viết một thuật toán hiệu quả sẽ giúp thời gian để xử lý logic giảm xuống tối thiểu nhất có thể.

2. Khái quát về độ phức tạp của thời gian

Độ phức tạp về thời gian được định nghĩa là lượng thời gian cần thiết để chạy một thuật toán. Nó đo thời gian thực hiện từng câu lệnh code trong một thuật toán. Thời gian được hiểu là số lần truy cập bộ nhớ được thực hiện, số lần so sánh giữa các số nguyên, số lần một số vòng lặp bên trong được thực thi hoặc một số đơn vị tự nhiên khác liên quan đến lượng thời gian thực mà thuật toán sẽ sử dụng.

Có nhiều loại độ phức tạp thời gian khác nhau được sử dụng, các loại phổ biến:
Constant time complexity

• Linear time complexity
• Logarithmic time complexity
• Quadratic time complexity
• Cubic time complexity

3. Làm thế nào để tìm độ phức tạp thời gian của thuật toán?

Bạn có thể tính độ phức tạp của thuật toán bằng cách phân tích các câu lệnh của chương trình. Tuy nhiên, bạn phải lưu ý cách sắp xếp giữa các câu lệnh vì yếu tố này ảnh hưởng đến thời gian chạy code của bạn. Chúng ta hãy cùng phân tích hướng giải quyết với từng trường hợp cụ thể dưới đây:

3.1. Sử dụng ký hiệu Big O

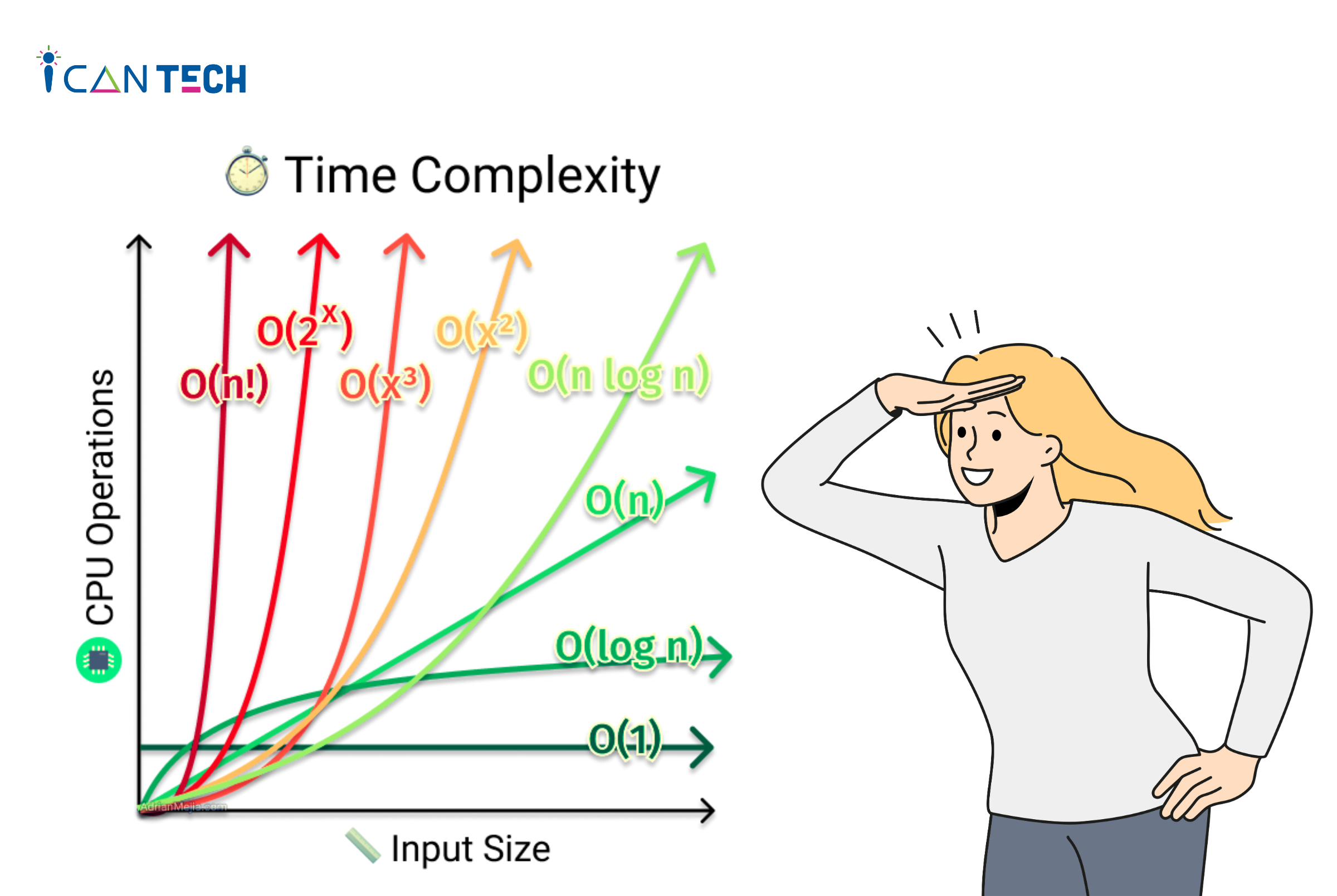
Sử dụng ký hiệu Big O là cách phổ biến nhất trong cách tính độ phức tạp của thuật toán về thời gian. Big O là một framework để phân tích và so sánh các thuật toán, hay khối lượng công việc mà CPU phải thực hiện. Ký hiệu Big O giúp loại bỏ các hằng số và các số hạng bậc thấp hơn. Ví dụ như O(3*n^2 + 10n + 10) trở thành O(n^2).

3.2. Tìm độ phức tạp của thuật toán với câu lệnh tuần tự

Nếu bạn đã có các câu lệnh với các thao tác cơ bản như so sánh, gán, đọc biến. Giả sử các câu lệnh này mất thời gian không đổi cho mỗi O(1). 

Ví dụ tính tổng bình phương của 3 số như sau:

function squareSum(a, b, c) {
const sa = a * a;
const sb = b * b;
const sc = c * c;
const sum = sa + sb + sc;
return sum;
}

Như bạn có thể thấy, mỗi câu lệnh là một phép toán cơ bản (toán và bài tập). Mỗi dòng mất thời gian không đổi O(1). Nếu chúng ta cộng tất cả các câu lệnh thì thời gian vẫn là O(1). Không quan trọng các số là 0 hay 9.007.199.254.740.991, nó vẫn sẽ thực hiện cùng một thao tác.

3.3. Với câu điều kiện

Rất hiếm khi bạn có một đoạn code mà không có bất kỳ câu lệnh điều kiện nào. Vậy làm thế nào để bạn biết cách xác định độ phức tạp của thuật toán? Bạn hãy xem ví dụ sau đây:

if (isValid) {
array.sort();
return true;

} else {
return false;
}

Ở ví dụ trên, khối if có thời gian chạy là O(n log n) (đó là thời gian chạy phổ biến cho các thuật toán sắp xếp hiệu quả). Khối else có thời gian chạy là O(1). Từ đó chúng ta có:
O([n log n] + [n]) => O(n log n)

Vì n log n có bậc cao hơn n nên chúng ta có thể biểu thị độ phức tạp thời gian là O(n log n).

3.4. Cách tính độ phức tạp của thuật toán với câu lệnh lặp

Một trong những tình huống bạn hay gặp là tính độ phức tạp của thuật toán với các vòng lặp for hoặc vòng lặp while.

Linear Time Loops 

Đối với bất kỳ vòng lặp nào, bạn cần tìm ra thời gian chạy của khối bên trong chúng và nhân nó với số lần chương trình sẽ lặp lại vòng lặp.

Ví dụ:

for (let i = 0; i < array.length; i++) {
statement1;
statement2;

}

Ở ví dụ trên, vòng lặp được thực thi array.length, giả sử n là độ dài của mảng, chúng ta có được kết quả như sau:

T(n) = n * [ t(statement1) + t(statement2) ]

Tất cả các vòng lặp tăng tỷ lệ thuận với kích thước đầu vào đều có độ phức tạp thời gian tuyến tính O(n). Nếu bạn chỉ lặp qua một nửa mảng thì đó vẫn là O(n). Do đã bỏ các hằng số nên chúng ta có 1/2 n => O(n).

Constant Time Loops 

Bạn hãy xem ví dụ dưới đây:

for (let i = 0; i < 4; i++) {
statement1;
statement2;
}

Mã code là O(1) vì nó không còn phụ thuộc vào kích thước đầu vào nữa. Code sẽ chạy câu lệnh 1 và 2 bốn lần.

Logarithmic Time Loops

Ví dụ:

function fn1(array, target, low = 0, high = array.length - 1) {
let mid;
while ( low <= high ) {
    mid = ( low + high ) / 2;
    if ( target < array[mid] )
high = mid - 1;
    else if ( target > array[mid] )
low = mid + 1;
    else break;
}
return mid;
}

Hàm này chia mảng cho điểm giữa của nó trên mỗi lần lặp. Vòng lặp while sẽ thực thi số lần mà chúng ta có thể chia array.length làm đôi. Bạn có thể đánh giá độ phức tạp của thuật toán bằng cách sử dụng hàm log. Ví dụ: nếu độ dài của mảng là 8 thì vòng lặp while sẽ thực thi 3 lần vì log2(8) = 3.

4. Lời Kết

Như vậy là với nội dung ở trên, chúng ta đã cùng nhau tìm hiểu về độ phức tạp của thuật toán và cách tính độ phức tạp về thời gian. Hi vọng rằng với những chia sẻ từ ICANTECH, bạn đã phần nào hiểu về độ phức tạp cũng như cách tính độ phức tạp của thuật toán. Bên cạnh đó, bạn cũng có thể tìm hiểu về chủ đề này qua cộng đồng chung của các lập trình viên để có thêm kinh nghiệm. 

Nếu bạn đang quan tâm đến học lập trình online thì hãy tham khảo ngay các khóa học lập trình tại ICANTECH nhé!

Nguồn ảnh: ICANTECH.