Hàm đệ quy là gì? Ứng dụng của hàm đệ quy trong C++

1. Tổng quan về đệ quy 

1.1. Hàm đệ quy là gì?

Ví dụ 1: Khi đặt 2 cái gương đối diện nhau và đứng ở giữa thì khi đó em có thể nhìn thấy:

• Trong cái gương thứ nhất có chứa hình ảnh của cái gương thứ hai.
• Ở hình ảnh của cái gương thứ 2 đó lại chứa hình ảnh của cái gương thứ nhất. Và nó cũng chứa tiếp hình ảnh của mình được phản chiếu trong hình ảnh của cái gương thứ nhất…

Ví dụ 2: Cách tính giai thừa của số n (n!)

• 0! = 1
• Nếu n>0 thì n! = n*(n-1)!

Hàm đệ quy (recursive function) là một hàm trong lập trình mà nó gọi chính nó trong quá trình thực thi. Điều quan trọng trong hàm đệ quy là có một điều kiện dừng, để ngăn hàm gọi chính nó vô hạn. Khi điều kiện dừng được đạt đến, quá trình đệ quy kết thúc.

Ví dụ:

HamDeQuy(){

      HamDeQuy();  //goi lai chinh no

}

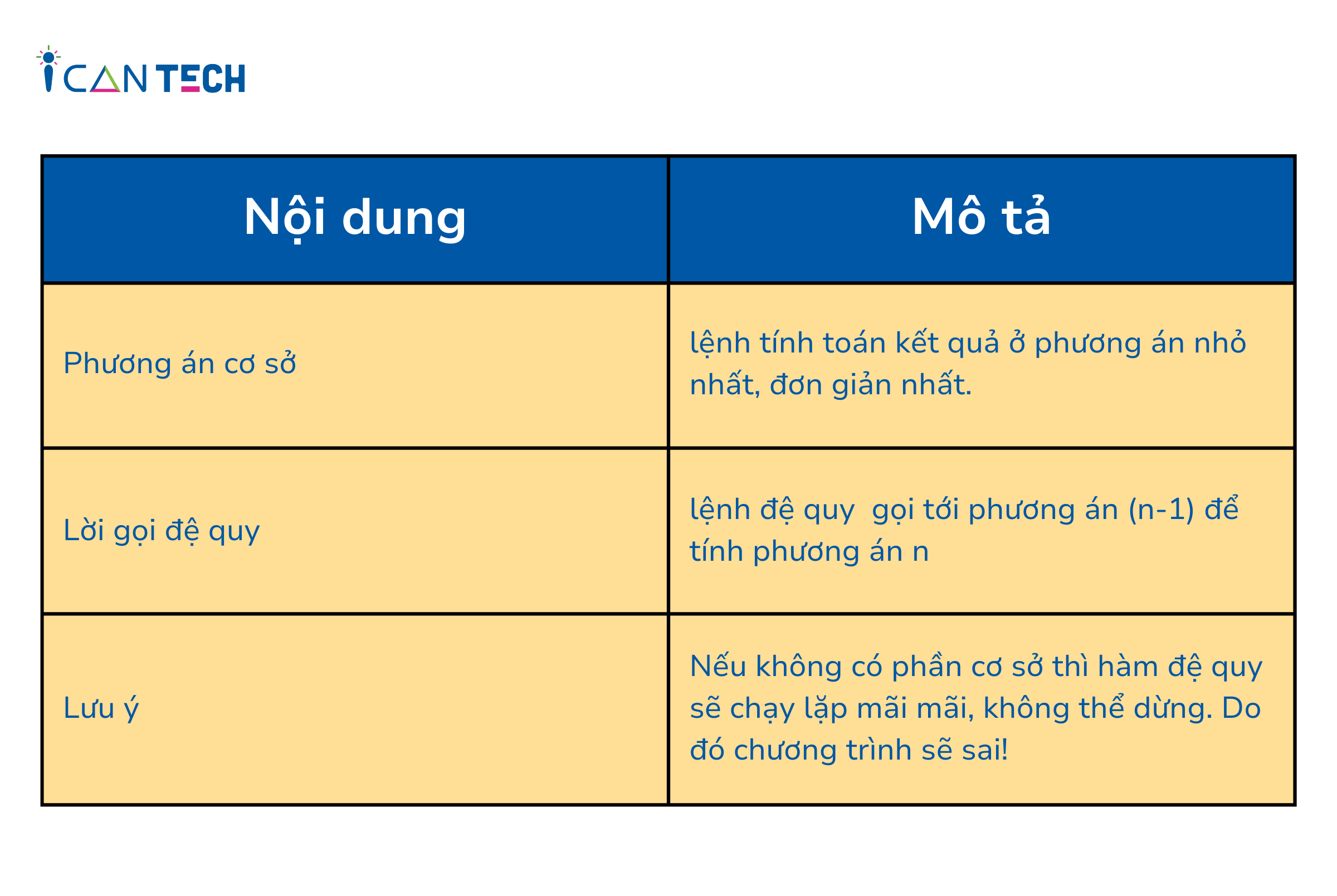
1.2. Đặc điểm của hàm đệ quy

1.3. Điều kiện dừng trong đệ quy

Trong đệ quy, điều kiện dừng (base case) là một điều kiện hoặc trạng thái đặc biệt mà khi nó được thoả mãn, quá trình đệ quy dừng lại và không gọi chính nó nữa. Điều kiện dừng quan trọng vì nó ngăn ngừa việc đệ quy chạy một cách vô hạn và đảm bảo rằng thuật toán sẽ dừng và trả về một kết quả.

Ví dụ về điều kiện dừng:

• Trong bài toán tính giai thừa, điều kiện dừng là khi n bằng 0 hoặc 1. Khi n là 0 hoặc 1, ta trả về 1 và không gọi đệ quy nữa.
• Trong bài toán tìm kiếm một phần tử trong một danh sách, điều kiện dừng có thể là khi danh sách rỗng hoặc khi đã tìm thấy phần tử cần tìm.
• Trong bài toán duyệt cây (tree traversal), điều kiện dừng có thể là khi đạt đến một nút lá (node lá) không có nút con.

2. Ứng dụng của hàm đệ quy trong C++

Dưới đây là một số ứng dụng của hàm đệ quy C++:

2.1. Tính giai thừa

2.1.1 Tính giai thừa sử dụng vòng for

Ý tưởng: Chúng ta sử dụng một vòng lặp for để tính giai thừa của số n. Chúng ta khởi tạo một biến result với giá trị ban đầu là 1 và sau đó sử dụng vòng lặp để nhân result với các số từ 1 đến n. Kết quả sau cùng là giai thừa của n.

#include <iostream>

int factorial(int n) {

    int result = 1;

    for (int i = 1; i <= n; i++) {

        result *= i;

    }

    return result;

}

int main() {

    int n;

    std::cout << "Nhập một số nguyên dương: ";

    std::cin >> n;

    if (n < 0) {

        std::cout << "Giai thừa không xác định cho số âm.\n";

    } else {

        int result = factorial(n);

        std::cout << n << "! = " << result << std::endl;

    }

    return 0;

}

Kết quả:

Nhập một số nguyên dương: 4

4! = 24

2.1.2 Tính giai thừa sử dụng hàm đệ quy trong C++

Ý tưởng: 

• Điểm dừng: Giai thừa của 0 là 1, và giai thừa của 1 cũng là 1. Đây là điểm dừng của đệ quy.
• Trong trường hợp chung, giai thừa của một số nguyên dương n (n > 1) có thể tính bằng cách nhân n với giai thừa của (n-1), tức là n! = n * (n-1)!.
• Sử dụng công thức sau:  n! = n * (n-1)!.

Ví dụ:

#include <iostream>

int factorial(int n) {

    // Điểm dừng

    if (n == 0 || n == 1) {

        return 1;

    }

    // Trường hợp chung

    return n * factorial(n - 1);

}

int main() {

    int n;

    std::cout << "Nhập một số nguyên dương: ";

    std::cin >> n;

    if (n < 0) {

        std::cout << "Giai thừa không xác định cho số âm.\n";

    } else {

        int result = factorial(n);

        std::cout << n << "! = " << result << std::endl;

    }

    return 0;

}

Kết quả:

Nhập một số nguyên dương: 3

3! = 6

Giả sử chúng ta cần tính kết quả của 3!, quy luật của đoạn code trên là::

• 3! = 2! * 3
• 2! = 1! * 2
• 1! = 1       

2.2.  Tìm phần tử thứ n trong dãy Fibonacci

2.2.1. Sử dụng vòng lặp for để tìm phần tử thứ n trong dãy  Fibonacci

Ý tưởng: Chúng ta sử dụng một vòng lặp for để tính số Fibonacci thứ n. Chúng ta khởi tạo hai biến fib1 và fib2 ban đầu là 0 và 1, và một biến result để lưu giá trị số Fibonacci tiếp theo. Chúng ta sử dụng vòng lặp để cập nhật giá trị của fib1 và fib2 dựa trên công thức Fibonacci (result = fib1 + fib2) và tiếp tục lặp qua các số Fibonacci cho đến khi đạt được số Fibonacci thứ n.

Ví dụ:

#include <iostream>

int fibonacci(int n) {

    if (n <= 1) {

        return n;

    }

    int fib1 = 0;

    int fib2 = 1;

    int result = 0;

    for (int i = 2; i <= n; i++) {

        result = fib1 + fib2;

        fib1 = fib2;

        fib2 = result;

    }

    return result;

}

int main() {

    int n;

    std::cout << "Nhập số n để tính dãy Fibonacci: ";

    std::cin >> n;

    if (n < 0) {

        std::cout << "Vui lòng nhập số không âm.\n";

    } else {

        int result = fibonacci(n);

        std::cout << "Phần tử thứ " << n << " trong dãy Fibonacci là: " << result << std::endl;

    }

    return 0;

}

Kết quả:

Nhập số n để tính dãy Fibonacci:6

Phần tử thú 6 trong dãy Fibonacci là: 8

2.2.2. Sử dụng hàm đệ quy để tìm phần tử thứ n trong dãy Fibonacci

Ý tưởng: Chúng ta sử dụng một hàm đệ quy fibonacci để tính số Fibonacci thứ n. Điều kiện dừng là khi n nhỏ hơn hoặc bằng 1, trong trường hợp này, chúng ta trả về n. Trong trường hợp khác, chúng ta gọi đệ quy với n - 1 và n - 2, sau đó cộng kết quả của hai cuộc gọi đệ quy lại với nhau để tính toán số Fibonacci thứ n.

Ví dụ:

#include <iostream>

int fibonacci(int n) {

    if (n <= 1) {

        return n;

    }

    return fibonacci(n - 1) + fibonacci(n - 2);

}

int main() {

    int n;

    std::cout << "Nhập số n để tính dãy Fibonacci: ";

    std::cin >> n;

    if (n < 0) {

        std::cout << "Vui lòng nhập số không âm.\n";

    } else {

        int result = fibonacci(n);

        std::cout << "Dãy Fibonacci thứ " << n << " là: " << result << std::endl;

    }

    return 0;

}

Kết quả:

Nhập số n để tính dãy Fibonacci:6

Phần tử thú 6 trong dãy Fibonacci là: 8

3. Lời Kết

Với bài viết trên, ICANTECH đã cùng bạn tìm hiểu hàm đệ quy là gì cũng như những cách sử dụng thuật toán này trong C++. Lưu ý trong quá trình lập trình, bạn nên cân nhắc trước khi sử dụng hàm đệ quy vì đôi khi có thể làm cho chương trình trở nên phức tạp hơn. 

Nếu bạn đang quan tâm đến học lập trình thì hãy tham khảo ngay các khóa học lập trình online tại ICANTECH nhé

Nguồn ảnh: ICANTECH.