Thuật toán tìm kiếm nhị phân là gì? Tìm hiểu về thuật toán tìm kiếm nhị phân

1. Tổng quan về bài toán tìm kiếm

1.1. Một số ví dụ về tìm kiếm

• Tìm kiếm điểm Toán của học sinh tên là ‘Nguyễn Anh Minh’.
• Tìm kiếm tên của học sinh.
• Tìm kiếm điểm ở cột tương ứng. 

1.2. Giới thiệu bài toán tìm kiếm

• Bài toán tìm kiếm:
  • Đầu vào: 
    • k: giá trị cần tìm 
    • X: dãy có n phần tử.
• Đầu ra: 
  • Vị trí của phần tử có giá trị k trong dãy X 
  • 0: nếu không tìm thấy

Ví dụ:

Đầu vào : 

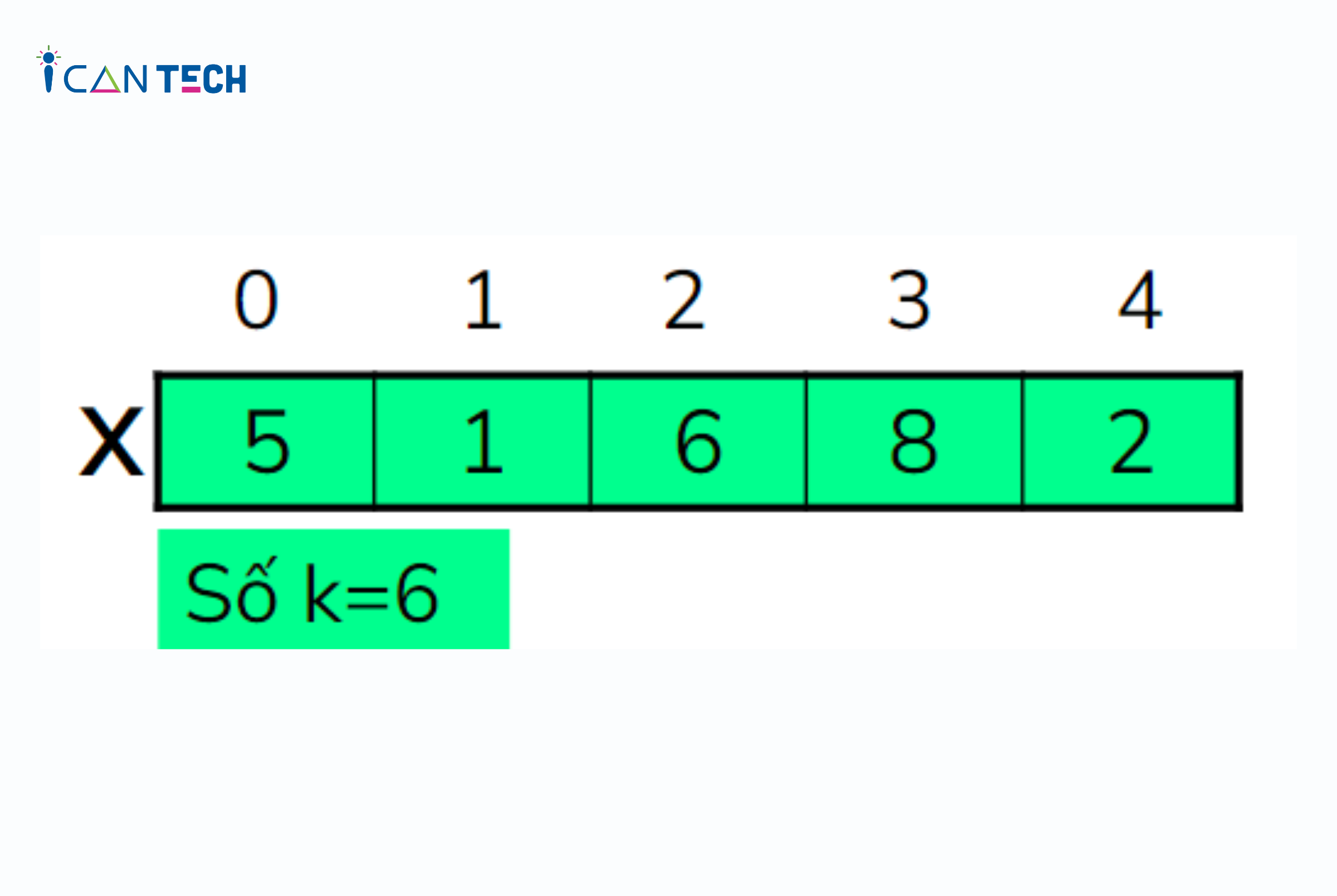
Đầu ra: 

2 (vị trí của số 6 trong dãy X)

2. Thuật toán tìm kiếm nhị phân

2.1. Ý tưởng thuật toán tìm kiếm nhị phân

“Thuật toán tìm kiếm nhị phân là gì?” là câu hỏi mà rất nhiều người quan tâm. Thuật toán tìm kiếm nhị phân (Binary Search) là một phương pháp hiệu quả để tìm kiếm một phần tử cụ thể trong một tập dữ liệu đã sắp xếp. Ý tưởng chính của thuật toán nhị phân là không phải kiểm tra từng phần tử một, mà là chia tập dữ liệu thành các phần nhỏ hơn và loại trừ một nửa của chúng sau mỗi bước.

Dưới đây là các bước cơ bản của thuật toán tìm kiếm nhị phân:

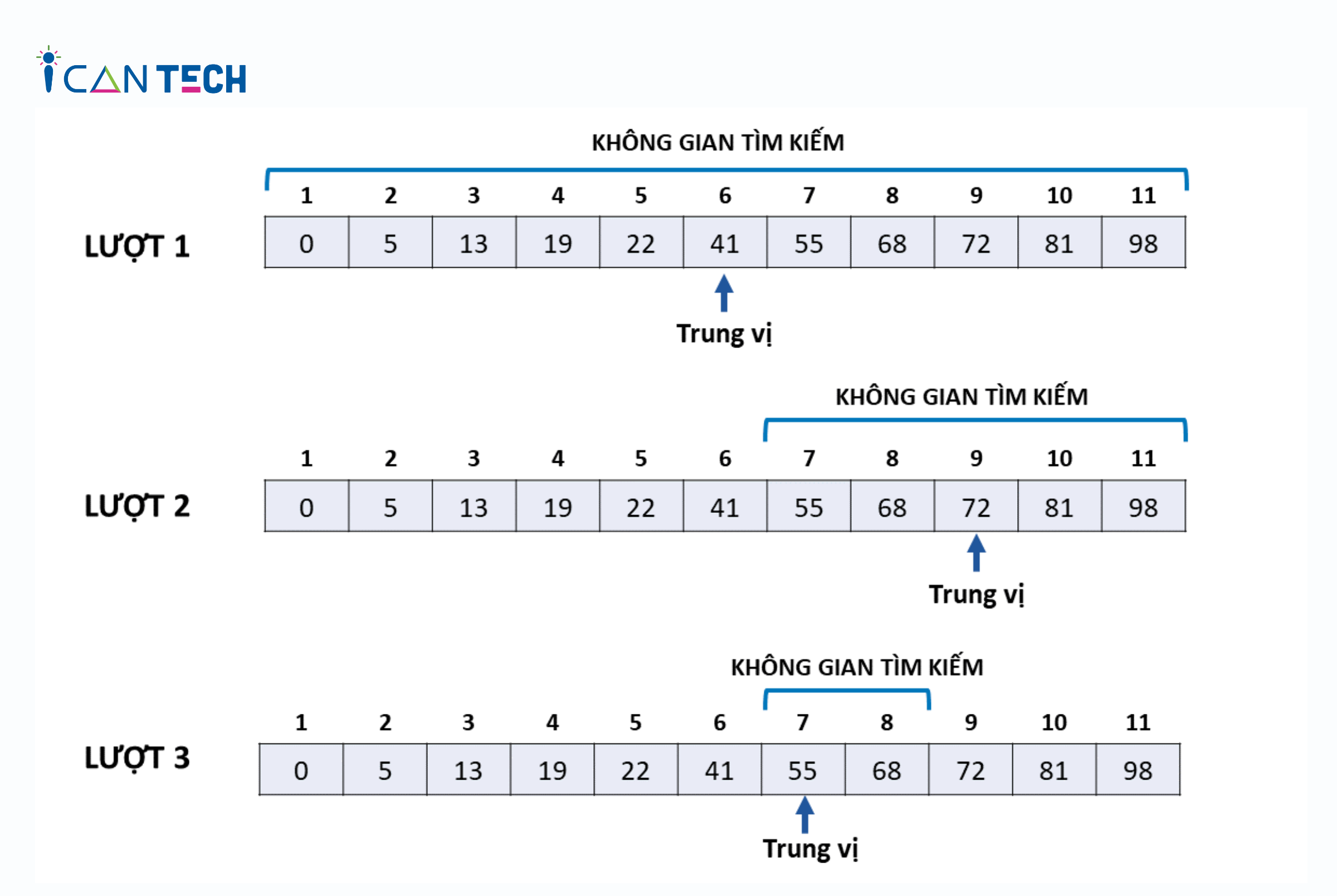
• Bước 1: Xác định phạm vi tìm kiếm: Bắt đầu bằng việc xác định phạm vi tìm kiếm ban đầu. Thông thường, phạm vi này ban đầu sẽ là toàn bộ tập dữ liệu (từ vị trí đầu tiên đến vị trí cuối).
• Bước 2: Tìm phần tử giữa: Tính toán chỉ số của phần tử ở giữa trong phạm vi tìm kiếm. Điều này thường được thực hiện bằng cách lấy trung bình của chỉ số đầu và chỉ số cuối.
• Bước 3: So sánh với phần tử giữa: So sánh phần tử tại vị trí giữa với giá trị cần tìm kiếm.

- Nếu phần tử giữa bằng giá trị cần tìm, thì tìm thấy và kết thúc tìm kiếm.

- Nếu phần tử giữa lớn hơn giá trị cần tìm, điều này có nghĩa rằng phần tử cần tìm nằm ở phía bên trái của phần tử giữa, vì tập dữ liệu đã sắp xếp. Do đó, thuật toán sẽ cập nhật phạm vi tìm kiếm cho phần bên trái của phần tử giữa và lặp lại quy trình trên phạm vi này.

- Nếu phần tử giữa nhỏ hơn giá trị cần tìm, tương tự, thuật toán sẽ cập nhật phạm vi tìm kiếm cho phần bên phải của phần tử giữa và tiếp tục tìm kiếm trên phạm vi này.

• Bước 4: Lặp lại quy trình: Lặp lại bước 2 và bước 3 cho đến khi tìm thấy phần tử cần tìm hoặc phạm vi tìm kiếm thu nhỏ đến một mức không thể thu nhỏ nữa.
• Bước 5: Kết thúc: Khi tìm thấy phần tử cần tìm hoặc phạm vi tìm kiếm đã thu nhỏ đến mức tối thiểu, thuật toán kết thúc.

Thuật toán tìm kiếm nhị phân hiệu quả vì sau mỗi bước, nó loại trừ một nửa của phạm vi tìm kiếm, giảm đáng kể số lần so sánh cần thực hiện, và có độ phức tạp thời gian trung bình là O(log n), trong đó "n" là số phần tử trong tập dữ liệu.

2.2. Code minh hoạ cho thuật toán tìm kiếm nhị phân bằng Python

def binary_search(arr, target):

    left, right = 0, len(arr) - 1

    while left <= right:

        mid = (left + right) // 2  # Tính toán chỉ số giữa

        if arr[mid] == target:

            return mid  # Tìm thấy giá trị, trả về chỉ số

        elif arr[mid] < target:

            left = mid + 1  # Cập nhật phạm vi tìm kiếm sang bên phải

        else:

            right = mid - 1  # Cập nhật phạm vi tìm kiếm sang bên trái

    return -1  # Không tìm thấy giá trị, trả về -1

# Ví dụ sử dụng

arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

target = 7

result = binary_search(arr, target)

if result != -1:

    print(f"Giá trị {target} được tìm thấy tại vị trí {result}.")

else:

    print(f"Giá trị {target} không tồn tại trong danh sách.")

3. Lời Kết

Thuật toán tìm kiếm nhị phân là một công cụ quan trọng trong việc giải quyết các vấn đề tìm kiếm, và được ứng dụng rộng rãi trong lập trình. 

Hi vọng rằng bài viết này của ICANTECH sẽ giúp bạn hiểu rõ cách hoạt động của thuật toán này và áp dụng vào các bài toán tương tự khác. Chúc các bạn thành công!

Nếu bạn đang quan đến học lập trình online thì hãy tham khảo ngay các khóa học lập trình tại ICANTECH nhé!
 

Nguồn ảnh: ICANTECH và Internet.